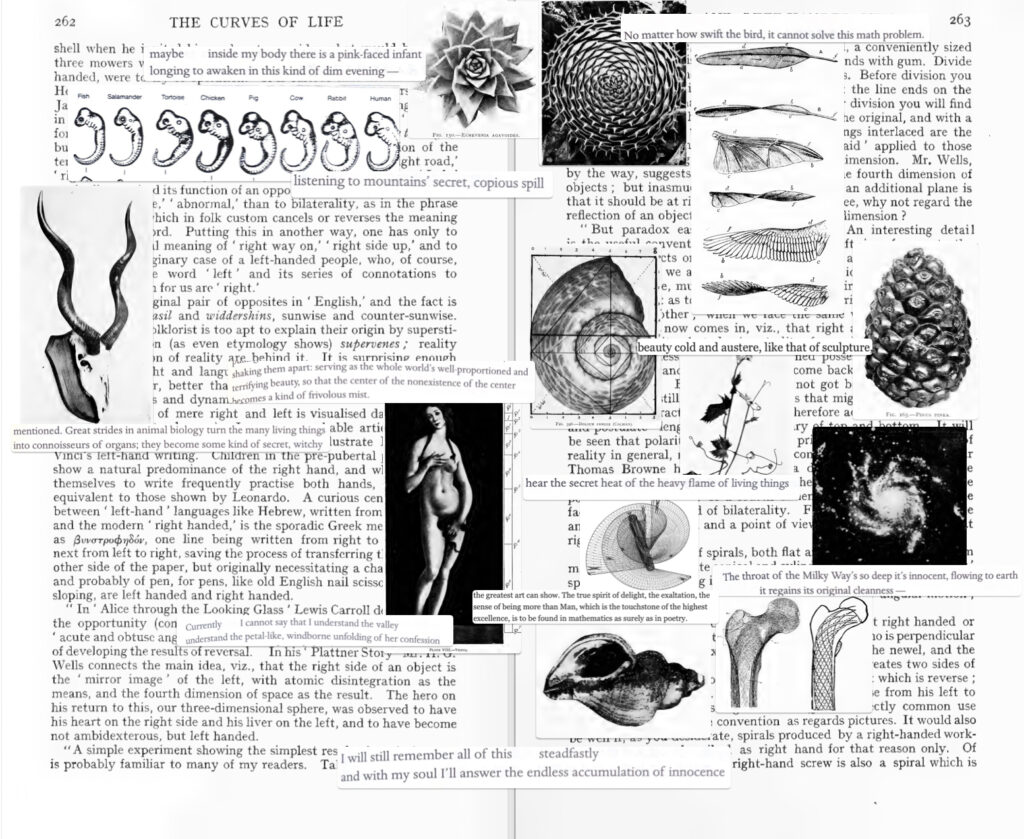
Reflection
The source material of my piece was Floral Mutter, a poetry collection by Chinese poet Ya Shi. I chose this poem because Ya Shi’s background as a mathematician and life in rural China provides complex and uniquely analytical meditations on nature. This blend of math and nature also reminded me of Fibonacci spirals, a childhood obsession of mine. The Curves of Life by Theodore Andrea Cook goes beyond Fibonacci spirals, and discusses all sorts of spirals and ratios that appear in nature. I chose to arrange photos showcasing spirals, mostly the Fibonacci spiral or golden ratio in nature, in the shape of a Fibonacci spiral. I cropped lines from Ya Shi’s poems and placed them aside images they matched and evoked a deeper meaning in. For example, next to the diagram of the spirals found in bird wings and feathers, I included the line “No matter how swift the bird, it cannot solve this math problem.” Though birds, like many living creatures, were selected for optimal survival in their environment, which meant the specific ratio of curve in their wings and feathers, they have no idea of the existence of the math ingrained in them. Nature wears math like an invisible cloak; aligning Ya Shi’s poetry with the scientific diagram illuminates the “math problem” in the poem and a more poetic meaning in the image. Though the arrangement of the images may look random at first, understanding of the mathematical basis behind it reveals the meaning behind it, just like the discovery of the Fibonacci spiral explaining phenomena in nature. I also dispersed Bertrand Russell’s quote from “The Study of Mathematics” throughout, since I think he presents a similar idea to my purpose for the piece. He compares math to having a particular beauty like poetry and I’ve put his conclusion in a new light by applying it to a specific math and specific poetry.
My purpose was to display themes of disorder in order, irrationality in the rational, and the innocence of math found in nature. The golden ratio is considered the most irrational number, because it can not be truncated in decimal form the way other irrational numbers can be. However, this irrationality is behind the most “perfect” composition in our eyes. Similarly, the pages in the background taken from The Curves of Life discuss right-handedness vs left-handedness. In it, Cook describes how left-handed Fibonacci spirals, despite still being the “perfect” composition, are seen as slightly unnatural compared to right-handed Fibonacci spirals. This is a very biased, human-specific view, and the overlay of images on top shows that nature does not care for favoring the left-side or right-side. Interestingly enough, Leonardo da Vinci, who utilized the golden ratio in his artwork, notably in the Vitruvian Man, was left-handed. Thus, another way of exemplifying how the most rational, “perfect”, orderly art comes from understandings of irrationality and unnaturalness.
My text is original because I’ve reinterpreted the meanings of images from The Curves of Life, text from The Curves of Life, lines from “The Study of Mathematics,” and lines from Floral Mutter. Rather than a superficial understanding, my knowledge of Ya Shi’s background and the math behind Fibonacci spirals informs a unique perspective of how to combine them. It’s less of a plagiarism than a reimagining of both works–it adds to the conversation rather than restating what both authors have already said.
Sources
Background: https://archive.org/details/cu31924028937179/page/262/mode/2up
Fibonacci turbine: https://cults3d.com/en/3d-model/gadget/fibonacci-wind-turbine?srsltid=AfmBOop8IcdIIgW8ivpAi5ijujafnkAr2AwA-GP9RCJdHOJWu9Ays5Mm
Poetry: Floral Mutter by Ya Shi
Quotes on math: https://users.drew.edu/~jlenz/br-ml-ch4.html